Legge di Ohm e dissipazione termica
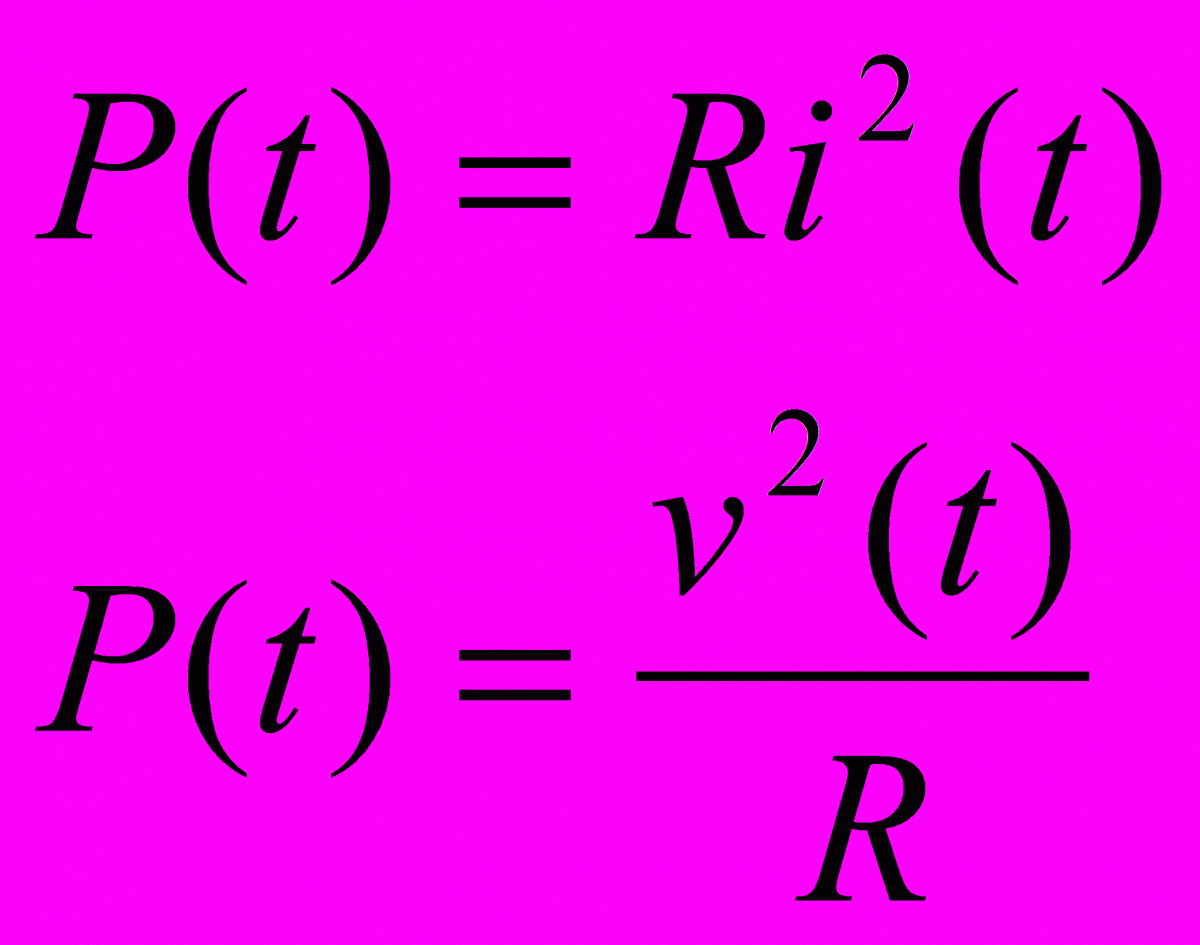
Oggi illustriamo un impiego pratico della legge di Ohm. Per mezzo delle formule proposte nel numero scorso, calcoleremo la corrente che scorre in una resistenza e la dissipazione termica del componente utilizzando un circuito molto semplice
Impiego pratico della legge di Ohm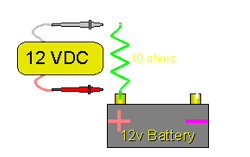
In “cos’è la corrente” abbiamo trattato la legge di Ohm e le relazioni che legano la tensione (V), la corrente (I), la resistenza (R) e la potenza (W). Oggi usiamo le formule che esprimono tali relazioni, che ci permetteranno di familiarizzare con la legge in questione. Inoltre analizzeremo l’aspetto della dissipazione termica. Nella figura è visibile un semplicissimo circuito: una resistenza da 10 Ohm collegata tra i poli positivo e negativo di una batteria da 12 Volt. Se al posto della resistenza ci fosse un tratto di conduttore elettrico ideale con resistenza nulla, e la batteria fosse una batteria ideale, avremmo nel circuito lo scorrimento di una quantità infinita di corrente. Ciò è verificabile per via matematica. Sul numero scorso infatti abbiamo espresso la corrente in termini di rapporto tensione/resistenza (3): I = V/R. Se, con V che rimane costante, facciamo tendere R a zero, la quantità I tenderà all’infinito. Ciò avrà come conseguenza un considerevole aumento di calore: il conduttore diventerà rovente e la guaina isolante probabilmente fonderà. La resistenza collegata tra i poli della batteria, invece, funziona da limitatore. Se inseriamo il suo valore, 10 Ohm, nella formula (3), la corrente che scorre nel circuito assume valori finiti: I = V/R = 12/10 = 1,2 Ampère. Tuttavia vi sarà ugualmente una certa produzione di calore. Per dimensionare adeguatamente il componente è necessario calcolare la potenza dissipata sotto forma di energia termica. Per farlo possiamo usare la formula che esprime la potenza in termini di tensione e resistenza: W = V²/R. Avremo allora: W = 12²/10 = 14,4 Watt. Allo stesso risultato si giunge utilizzando un’altra formula, che esprime la potenza come prodotto tra il quadrato della corrente e la resistenza: W = I²R = (1,2)² x 10 = 14,4 Watt. Se la potenza dissipata è di 14,4 Watt, per rimanere entro i margini di sicurezza sarà bene usare una resistenza da 30 Watt. Come ulteriore esperimento possiamo calcolare la corrente e la dissipazione di potenza che si hanno portando il valore della resistenza a 22 Ohm e mantenendo costante la tensione a 12 Volt. Per semplicità omettiamo i passaggi e riportiamo i valori finali: I = 0,54 Ampère e W = 6,54 Watt. Quindi sarà bene usare una resistenza di almeno 12/15 Watt.

Semplice circuito costituito da una resistenza da 10 Ohm collegata tra i poli positivo e negativo di una batteria da 12 Volt. Con tali parametri, nel circuito scorre una corrente di 1,2 Ampère; la potenza dissipata dalla resistenza sotto forma di calore è di 14,4 Watt.



